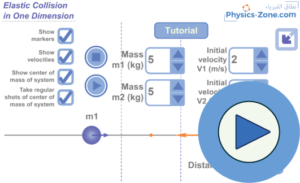
دليل المحاكاة: التصادم المرن الأحادي البعد
Are you interested in translating this manual into another language? Please contact me here.
To read the English version click here.
لتنزيل هذا الدليل بصيغة pdf أنقر هنا.
مقدمة:
توضح هذه المحاكاة قوانين الانحفاظ في التصادمات المرنة أحادية البعد، وهي: قانون انحفاظ الزخم الخطي وقانون انحفاظ الطاقة الحركية.
عندما يتم تعيين العوامل الأولية (كتل الكرات، وسرعاتها الأولية)، يمكن تحديد السرعات النهائية، وستلاحظ تحرك الكرات المتصادمة وفقًا لذلك.
كما توضح هذه المحاكاة فكرة أخرى، وهي أن مركز كتلة الأنظمة المعزولة يستمر في التحرك بنفس السرعة قبل الاصطدام وبعده. لإظهار ذلك، هناك خيار لأخذ لقطات متتالية لمركز كتلة النظام المكون من الكرتين على فترات زمنية متساوية، ويتم توفير علامتين (خطين عامودين قابلين للسحب) لقياس المسافة بين نقطتي الطباعة المتتالية، حتى تتمكن من التحقق أن المسافات بين هذه النقاط المتتالية متساوية، وبالتالي فإن مركز الكتلة يغطي مسافات متساوية خلال فترات زمنية متساوية، مما يعني أن سرعته ثابتة.
المستخدِمون المستهدَفون:
تعتبر هذه المحاكاة مفيدة عمليا وعلميا للطلاب الذين يرغبون في إجراء التجربة افتراضيا دون اللجوء إلى مختبر حقيقي (أو في حالة نقص معدات المختبر).
وهي أيضا محاكاة قيمة وعملية للمعلمين ومدرسي المختبرات الذين يرغبون في إشراك طلابهم في أداء الأنشطة المخبرية والخروج بالاستنتاجات واكتشاف المبادئ الأساسية.
نصيحتي للمدرسين الذين يرغبون بالاستفادة من هذه المحاكاة أن يقدموها بنهج الاكتشاف الموجه. بهذه الطريقة، يُوجّه التلاميذ من خلال تكرار التجربة لاكتشاف المبادئ الأساسية بدلا من تلقيها.
أهمية المحاكاة:
تعتبر تجربة الاصطدام المرن إحدى تجارب الفيزياء المعقدة. حيث يتم إجراؤها عادةً على طاولة هوائية أو على مسار هوائي، وكلاهما معدات مكلفة وتتطلب الكثير من التحضير والقياس الدقيق. ولا يمكن العثور على هذه المعدات بسهولة في كل مختبر مدرسي. لذلك، تسهل هذه المحاكاة على طلاب المدارس الثانوية والمرحلة الجامعية الأولى أداء نشاط ميسور التكلفة يُمكّنهم من اكتساب المهارات والمعرفة المطلوبة في هذا الموضوع.
لا شك أنه من الأفضل إجراء تجربة حقيقية بدلاً من التجربة الافتراضية عندما يكون ذلك ممكنًا. ومع ذلك، فإن للتجربة الافتراضية أهمية كبيرة في حالة نقص المعدات أو لنشاط أولي لإعداد الطلاب للمختبر الحقيقي.
كذلك قد يجد المصممون التعليميّون ومنشئو الدورات التدريبية هذه المحاكاة أداة مساعدة في تسهيل عملهم.
مقدمة قصيرة لقوانين الانحفاظ في الاصطدامات:
قانون انحفاظ الزخم الخطي لنظام معزول:
ينص هذا القانون على أن الزخم الخطي الكلي لنظام معزول مُنحفظ (لا يتغير).
المقصود بالنظام المعزول نظام يتكون من جسيمين أو أكثر قد تتفاعل مع بعضها البعض، ولكنها لا تتفاعل مع أي جسيمات أخرى. ونظرًا لأنها لا تتفاعل مع أي جسيمات أخرى، فهذا يعني إما أنه لا توجد قوة خارجية تؤثر على هذا النظام، أو أن القوى الخارجية على النظام تلغي بعضها البعض بحيث يكون مجموع القوى الخارجية صفرًا. رياضيا نكتب القانون على النحو التالي:
حيث هو مجموع القوى الخارجية المؤثرة على النظام، و
هو الزخم الخطي الكلي للنظام، كما أننا نقصد بـ
متجه ثابت.
أثناء الاصطدام، يكون الزخم الخطي الكلي للجسيمات المتصادمة مُنحفظا. وهذا يعني أنه يبقى ثابتًا قبل وبعد الاصطدام. وهذا صحيح بشكل عام حتى ولو كانت الجسيمات المتصادمة خاضعة لقوى خارجية مثل الوزن أو الاحتكاك (وبالتالي لا يكون النظام معزولًا). وذلك لأن القوى الخارجية مثل وزن الكرات أو الاحتكاك لا تكاد تذكر مقارنة بالقوى الداخلية التي حدثت بين الجسيمات أثناء الاصطدام. لذلك، كتقريب، يعتبر النظام معزولًا فقط أثناء الاصطدام (الذي يستمر لفترة زمنية قصيرة جدًا). في هذه الحالة، نستطيع القول أن الزخم الخطي الكلي للنظام قبل الاصطدام مباشرة وبعد الاصطدام مباشرة منحفظ. رياضيا:
في حالة تجربة هذه المحاكاة:
حيث و
هما على التوالي السرعات الابتدائية للكرة 1 (ذات الكتلة m1) والكرة 2 (ذات الكتلة m2)، و
و
هما على التوالي السرعات النهائية للكرة 1 والكرة 2 (من الآن فصاعدًا لنسميهما m1 و m2 للاختصار).
في تصادم أحادي البعد، يمكن استبدال متجهات السرعة ،
،
، و
بقيمها الجبرية
،
،
، و
على المحور السيني:
قانون انحفاظ الطاقة الحركية أثناء الاصطدام المرن:
علاوة على ذلك، إن لم يكن هناك تبديد للطاقة أثناء التصادم على شكل حراري أو بسبب التشوه الدائم للجسيمات المتصادمة أو في شكل إشعاع وما إلى ذلك، فيُقال إن التصادم مرن. في هذه الحالة، تنحفظ الطاقة الحركية الكلية للجسيمات المتصادمة قبل الاصطدام وبعده مباشرة. رياضيا:
حيث Kbefore هي الطاقة الحركية الكلية للجسيمات المتصادمة قبل الاصطدام مباشرة، و Kbefore هي الطاقة الحركية الكلية للجسيمات المتصادمة بعد الاصطدام مباشرة.
في حالة تجربة هذه المحاكاة:
حيث و
هما على التوالي القيم الجبرية للسرعات الأولية لكل من m1 و m2 و
و
هما على التوالي القيم الجبرية للسرعات النهائية لكل من m1 و m2.
التصادم المرن:
بدمج قانونَي الانحفاظ أثناء التصادم المرن، يمكننا تحديد السرعات النهائية للجسيمين المتصادمين لكتل معينة بعد الاصطدام مباشرة إذا كانت السرعات الأولية للجسيمين معروفة قبل الاصطدام مباشرة. بعد بعض المعالجات الرياضية للمعادلتين:
و
يمكنك إيجاد القيم الجبرية للسرعات النهائية بدلالة الكتل m1 و m2 والقيم الجبرية للسرعات الابتدائية:
ملاحظات:
في هذه المحاكاة، يمكنك أيضًا التحقق من حالتين خاصتين:
1. إذا كان الجُسيمان متساويان في الكتلة، فعند التعويض في التعبيرين المذكورين أعلاه للسرعتين النهائيتين، نجد أن الجُسيمين يتبادلان السرعات:
2. إذا كان الجسيمان متساويان في الكتلة وكان الجسيم الثاني في حالة سكون ابتداءً، فإنهما يتبادلان السرعات، وبالتالي بعد الاصطدام، يتوقف الجسيم الأول ويعطي سرعته للجسيم الثاني:
حركة مركز الكتلة لنظام معزول:
يساوي الزخم الخطي لنظام من الجُسيمات ذات الكتلة الثابتة الزخم الخطي الخاص بمركز كتلته G، حيث يُفترض أن الكتلة الكلية مُركّزة في مركز الكتلة. في حالة النظام المعزول، يكون الزخم الخطي للنظام ثابتًا وبالتالي تظل سرعة مركز الكتلة G للنظام ثابتة. ومن ثم، فإن مركز الكتلة لنظام معزول يتحرك بسرعة ثابتة على طول خط مستقيم. رياضيا:
حيث هو الزخم الخطي الكلي لـلنظام. M هي الكتلة الكلية للنظام، و
هي سرعة مركز كتلة النظام.
في حالة النظام المعزول:
وبالتالي، يتحرك مركز الكتلة G بسرعة منتظمة.
إرشادات العمل الخاصة بالمحاكاة:
في هذا القسم، سنستعرض كل عنصر من عناصر المحاكاة ونوضح وظيفتها.
لاحظ أنه يمكنك أيضًا استعراض هذا البرنامج التعليمي في المحاكاة بالنقر فوق الزر البرنامج التعليمي “Tutorial”.
1. تكبير / تصغير زر التبديل: انقر على هذا الزر للتبديل بين وضع ملء الشاشة واستعادة وضع النافذة.
2. m1 و m2: هذه هي الكرات المتصادمة ذوات كتل m1 و m2 (m1 و m2 تُحدد مسبقا من قِبَل المُستخدم). عندما تبدأ التجربة، سوف تتحرك بسرعات يحددها مسبقا المستخدم أيضًا. لاحظ أنها تصطدم بمرونة، وبذلك يتم تطبيق قانون انحفاظ الزخم الخطي وقانون انحفاظ الطاقة الحركية أثناء التصادم.
3. المحور السيني: هذا هو المحور الذي تتحرك عليه الكرتان. تذكر أن التجربة أحادية البعد، لذا فإن كل كرة ستتحرك إما لليسار أو لليمين.
4. زر التشغيل: عند الانتهاء من ضبط عوامل التجربة (كتل الكرتين m1 و m2 ، وسرعتهما V1 و V2) ، انقر على هذا الزر لبدء حركة الكرتين.
5. زر إعادة التعيين / الإيقاف: انقر على هذا الزر لإيقاف التجربة الحالية وإرجاع الكرتين إلى موضعهما الأولي، دون إعادة ضبط كتلتهما أو سرعتهما.
6. زر الاختيار “إظهار السرعات”: اضغط على زر الاختيار هذا لإظهار متجهات السرعة على كل من الكرتين.
7. زر الاختيار “إظهار مركز كتلة النظام”: اضغط على زر الاختيار هذا لإظهار مركز كتلة الكرتين أثناء تحركهما.
8. زر الاختيار “أخذ لقطات منتظمة لمركز كتلة النظام”: اضغط على زر الاختيار هذا لاستنساخ مركز كتلة الكرتين على المحور السيني بشكل دوري (كل فترة زمنية ثابتة). يوضح ذلك لك أن مركز الكتلة يغطي مسافات متساوية في كل فترة زمنية متساوية
9. زر الاختيار “إظهار العلامات”: ضع علامة على زر الاختيار هذا لتمكين رؤية العلامتين الرأسيتين (خطين عامودين قابلين للسحب). عندما تريد قياس المسافة بين موضعين على المحور x، اسحب هذين الخطين وضع أحدهما في موضع والثاني في الموضع الآخر، فسترى المسافة بين هذين الموضعين معروضة داخل مربع النص المسمى “مسافة”.
10. مربع النص “مسافة”: يعرض مربع النص هذا المسافة بين العلامتين الرأسيتين على المحور x. يفيد ذلك في قياس المسافة بين نقطتين متتاليتين لمركز كتلة النظام المكون من الكرتين ولإثبات أنهما متباعدتان بشكل متساوٍ وبالتالي يتحرك مركز الكتلة بسرعة منتظمة.
11. زر التعديل “Mass m1“: استخدم هذا الزر لزيادة أو إنقاص الكتلة m1 للكرة 1 بمقدار 1 كجم في كل خطوة.
12. زر التعديل “Mass m2“: استخدم هذا الزر لزيادة أو إنقاص الكتلة m2 للكرة 2 بمقدار 1 كجم في كل خطوة.
13. زر التعديل “السرعة الابتدائية V1“: استخدم هذا الزر لزيادة أو إنقاص سرعة الكرة m1 بمقدار 1 م/ث في كل خطوة. لاحظ أن السرعة الموجبة تعني أن الكرة تتحرك في الاتجاه الموجب (إلى اليمين)، بينما تعني السرعة السالبة أن الكرة تتحرك في الاتجاه السالب (إلى اليسار).
14. زر التعديل “السرعة الابتدائية V2“: استخدم هذا الزر لزيادة أو إنقاص سرعة الكرة m2 بمقدار 1 م/ث في كل خطوة. لاحظ أن السرعة الموجبة تعني أن الكرة تتحرك في الاتجاه الموجب (إلى اليمين)، بينما تعني السرعة السالبة أن الكرة تتحرك في الاتجاه السالب (إلى اليسار).
15. “السرعة الابتدائية لـ m1“: قبل الاصطدام، يعرض هذا النص السرعة الابتدائية لـ m1.
16. “السرعة الابتدائية لـ m2“: قبل الاصطدام، يعرض هذا النص السرعة الابتدائية لـ m2.
17. “السرعة النهائية لـ m1“: بعد الاصطدام، يعرض هذا النص السرعة النهائية لـ m1.
18. “السرعة النهائية لـ m2“: بعد الاصطدام، يعرض هذا النص السرعة النهائية لـ m2.
خاتمة:
من خلال هذه المحاكاة الغنية بعناصر التحكم والمرئيات لتوضيح قوانين الانحفاظ في التصادم أحادي البعد، وباستخدام المنهجيات التعليمية المناسبة، ستتوفر الفرصة للمدرس لتنمية روح الاكتشاف لدى المتعلمين وتقديم مفهوم التصادم في عرض تقديمي بسيط وواضح وغني بالمرئيات ولتمكين المتعلمين من اكتساب الأهداف التعلمية المطلوبة.
وقد تمت برمجة هذه المحاكاة بأحدث أدوات الويب HTML5 / JavaScript.